Блог для уроків інформатики: Тригонометричні рівняння

понедельник, 23 февраля 2015 г.

Тригонометричні рівняння

Арктангенс
Арктангенс, y = arcsin x, определен при $-\infty \leqslant x \leqslant \infty$ и имеет множество значений $- \frac{\pi}2 \leqslant y \leqslant \frac{\pi}2$ .
График функции арктангенс

График функции y = arctg xГрафик арктангенса получается из графика тангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, множество значений ограничивают интервалом $- \frac{\pi}2 \leqslant y \leqslant \frac{\pi}2$ , на котором функция монотонна. Такое определение называют главным значением арктангенса.
Арккотангенс

Арккотангенс,   y = arcctg x, определен при    $-\infty \leqslant x \leqslant \infty$ и имеет множество значений $0 \leqslant y \leqslant \pi$ .
График функции арккотангенс

График функции   y = arcctg xГрафик арккотангенса получается из графика котангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом    $0 \leqslant y \leqslant \pi$ , на котором функция монотонна. Такое определение называют главным значением арккотангенса.
Четность
Функция арктангенс является нечетной:
arctg(–x) = arctg(–tg arctg x) = arctg(tg(–arctg x)) = – arctg xФункция арккотангенс не является четной или нечетной:
arcctg(–x) = arcctg(–ctg arcctg x) = arcctg(ctg(π–arcctg x)) =π – arcctg x ≠ ± arcctg x.
Свойства - экстремумы, возрастание, убывание
Основные свойства арктангенса и арккотангенса представлены в таблице.

y = arctg x y = arcctg x

Область определения – ∞ ≤ x ≤ ∞ – ∞ ≤ x ≤ ∞

Множество значений $-\frac{\pi}2 \leqslant y$ $\leqslant \frac{\pi}2$ $0 \leqslant y \leqslant \pi$

Возрастание, убывание монотонно возрастает монотонно убывает

Максимумы, минимумы нет нет

Нули, y = 0 x = 0 нет

Точки пересечения с осью ординат, x = 0 y = 0 y = π/2

$\lim\limits_{x\to -\infty}{y(x)}$ – $\frac{\pi}2$ π

$\lim\limits_{x\to +\infty}{y(x)}$ $\frac{\pi}2$ 0

Таблица арктангенсов и арккотангенсов
В данной таблице представлены значения арктангенсов и арккотангенсов, в градусах и радианах, при некоторых значениях аргумента.

x arctg x arcctg x

град. рад. град. рад.

– ∞ – 90° – $\frac{\pi}2$ 180° π

– $\sqrt{3}$ – 60° – $\frac{\pi}3$ 150° $\frac{5\pi}6$

– 1 – 45° – $\frac{\pi}4$ 135° $\frac{3\pi}4$

– $\frac{1}{\sqrt3}$ – 30° – $\frac{\pi}6$ 120° $\frac{2\pi}3$

0 0° 0 90° $\frac{\pi}2$

$\frac{1}{\sqrt3}$ 30° $\frac{\pi}6$ 60° $\frac{\pi}3$

1 45° $\frac{\pi}4$ 45° $\frac{\pi}4$

$\sqrt{3}$ 60° $\frac{\pi}3$ 30° $\frac{\pi}6$

+ ∞ 90° $\frac{\pi}2$ 0° 0

Арксинус
Арксинус,   y = arcsin x   определен при    $-1 \leqslant x \leqslant 1$    и имеет множество значений $- \frac{\pi}2 \leqslant y \leqslant \frac{\pi}2$ .
График функции арксинус

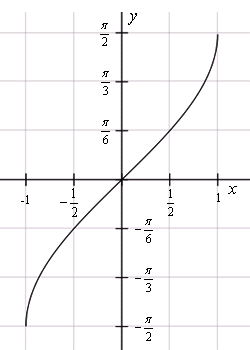
График функции   y = arcsin xГрафик арксинуса получается из графика синуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом    $- \frac{\pi}2 \leqslant y \leqslant \frac{\pi}2$ , на котором функция монотонна. Такое определение называют главным значением арксинуса.
Арккосинус
Арккосинус,   y = arccos x   определен при    $-1 \leqslant x \leqslant 1$    и имеет множество значений $0 \leqslant y \leqslant \pi$ .
График функции арккосинус

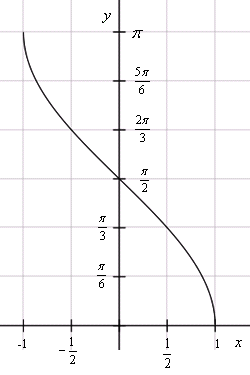
График функции   y = arccos xГрафик арккосинуса получается из графика косинуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом    $0 \leqslant y \leqslant \pi$ , на котором функция монотонна. Такое определение называют главным значением арккосинуса.
Четность
Функция арксинус является нечетной:
arcsin(–x) = arcsin(–sin arcsin x) = arcsin(sin(–arcsin x)) = – arcsin xФункция арккосинус не является четной или нечетной:
arccos(–x) = arccos(–cos arccos x) = arccos(cos(π–arccos x)) =π – arccos x ≠ ± arccos x Свойства - экстремумы, возрастание, убывание
Основные свойства арксинуса и арккосинуса представлены в таблице.

y = arcsin x y = arccos x

Область определения – 1 ≤ x ≤ 1 – 1 ≤ x ≤ 1

Область значений $-\frac{\pi}2 \leqslant y$ $\leqslant \frac{\pi}2$ $0 \leqslant y \leqslant \pi$

Возрастание, убывание монотонно возрастает монотонно убывает

Максимумы    $y = \frac{\pi}2$    $y = \pi$

Минимумы    $y = -\frac{\pi}2$

Нули, y = 0 x = 0 x = 1

Точки пересечения с осью ординат, x = 0 y = 0 y = π/2

Таблица арксинусов и арккосинусов
В данной таблице представлены значения арксинусов и арккосинусов, в градусах и радианах, при некоторых значениях аргумента.

x arcsin x arccos x

град. рад. град. рад.

– 1 – 90° – $\frac{\pi}2$ 180° π

– $\frac{\sqrt{3}}2$ – 60° – $\frac{\pi}3$ 150° $\frac{5\pi}6$

– $\frac{\sqrt{2}}2$ – 45° – $\frac{\pi}4$ 135° $\frac{3\pi}4$

– $\frac{1}2$ – 30° – $\frac{\pi}6$ 120° $\frac{2\pi}3$

0 0° 0 90° $\frac{\pi}2$

$\frac{1}2$ 30° $\frac{\pi}6$ 60° $\frac{\pi}3$

$\frac{\sqrt{2}}2$ 45° $\frac{\pi}4$ 45° $\frac{\pi}4$

$\frac{\sqrt{3}}2$ 60° $\frac{\pi}3$ 30° $\frac{\pi}6$

1 90° $\frac{\pi}2$ 0° 0

Комментариев нет:

Отправить комментарий

Подписаться на: Комментарии к сообщению (Atom)